Introduction

The notion of reducing the exposure of personnel even below the legally required limits is deeply embedded in both the EU and IAEA Basis Safety Standards and has been included in the German Radiation Protection Ordinance, Strahlenschutzverordnung (since 2019: Radiation Protection Law, Strahlenschutzgesetz). This reduction may be accomplished by technical, (civil) engineering and organisational measures, as addressed in the following examples: The number and thickness of walls is chosen to be commensurate to the expected gamma activity in the facility, in order to attenuate gamma radiation even below the limits. Technical measures may include reduction of the activity inventory in the waste packages. Finally, organisational measures such as rotating shift systems prevent individual employees from working at high dose locations for long periods of time.

During the operation of a storage facility the dose rate distribution (dose rate cadastre) is dynamic, changing with every newly emplaced and removed waste package. Additional dose reducing measures operators have at their disposal are the positioning of new waste packages in the facility, or even rearrangement of waste packages to achieve the largest possible shielding absorption effect by other packages. While numerous other constraints, especially of logistical nature, must be respected, the operator may want to reduce the overall dose rate by rearranging some or all waste packages at the time of emplacement or removal. In principle, the decision where to place new waste packages is not trivial; the minimum dose rate arrangement depends on the radiological properties of all packages in a non-linear fashion.

While the placement of individual packages that will lead to the minimum dose rate may be decided upon based on a quantitative assessment, the author is unaware of any study in which all the waste packages’ positions may so be changed as to minimize a dose rate. In [1], an arrangement of non-attenuating single-sources in one dimension was identified which reduced the dose rate at a calculation point perpendicular to this line.

In this article, we numerically identify dose-minimized drum arrangements using a state-of-the-art optimizer, permitting all drums of the storage facility to change position. The storage facility in question hosts a large number of drums with an appreciable dose rate (up to 100 Sv/h), causing skyshine, which in turn results in an appreciable dose rate even outside the building of the facility. The goal of this study is to identify new drum arrangements that reduce the dose rate above the storage cells in the facility and ultimately the dose rate in the far-field.

Basic considerations

Consider three waste drums of similar activity and density (for simplicity, we will assume that the waste contains just one gamma-emitting radionuclide, e. g. Co-60): Drum 1 has a fixed position, its radiological properties (activity and density) are well defined. In addition, the radiological properties of drum 2 are fixed. Only the properties of drum 3 are not well known; however, drum 3 shall always have a higher dose rate than drum 2. Both drums can take positions either directly above drum 1 or immediately adjacent to drum 1 (Figure 1, left). The question at hand is what the dose minimizing arrangement of drum 2 and drum 3 is at a calculation point above the drums (the eye in Figure 1).

Intuitively, one might shield drum 1 by the low dose rate drum 2, placing it on top of drum 1, regardless of other radiological properties. That is often, but not always the correct decision for a dose-minimal configuration, as shown in Figure 1, right. Here, we show the dose rate benefit obtained for drum 3 used as shielding with respect to drum 2. For a large region of parameter space, the benefit is negative (blue area), that is, the intuition is correct: It is worse to use drum 3 as shielding with respect to drum 2. However, for certain combinations of activity and density of drum 3, it should be used as shielding, despite its higher dose rate (red area). The hatched area is parameter space for which the dose rate of drum 2 is higher than that of drum 3.

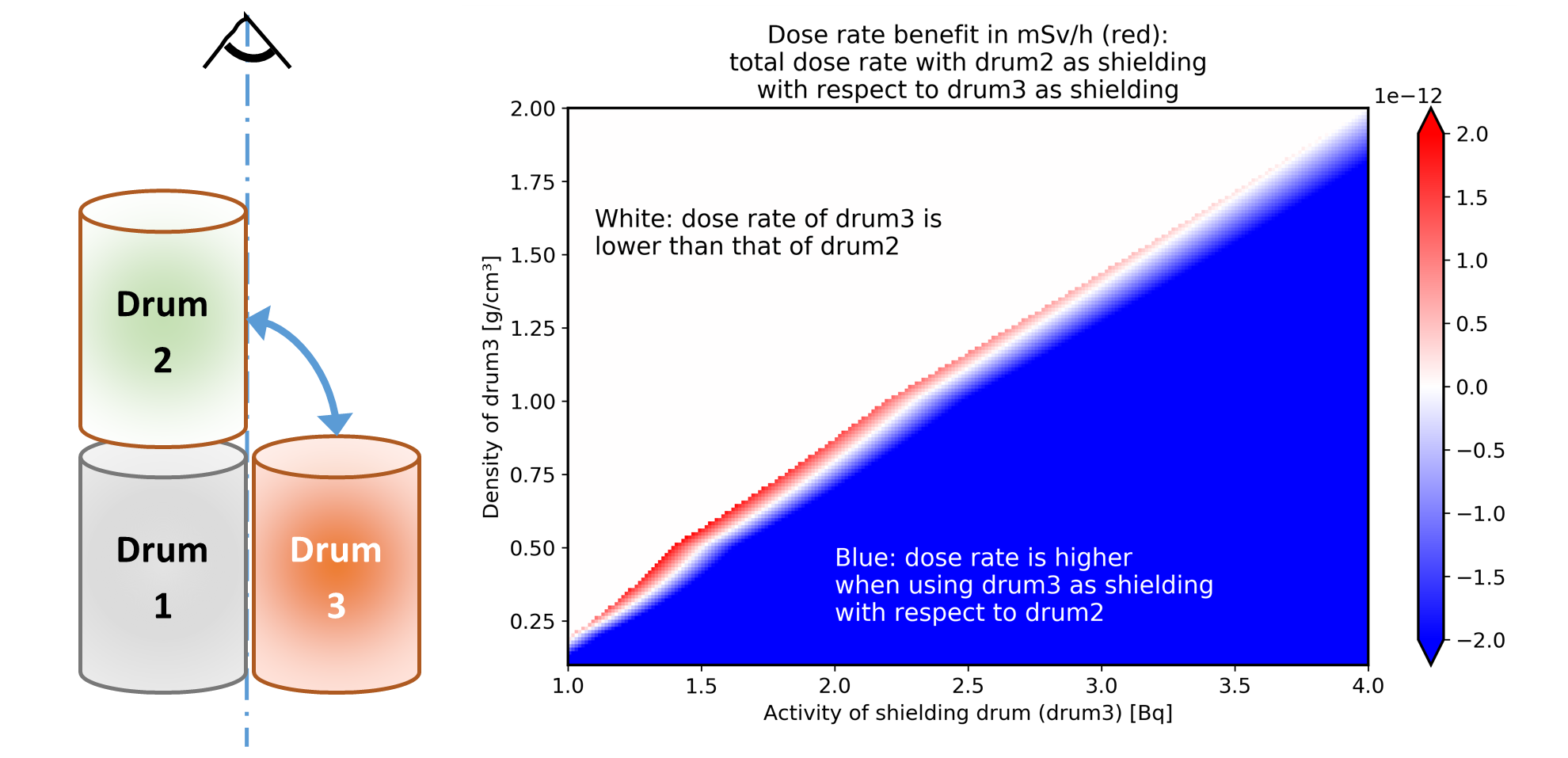
Figure 1: Simple arrangement possibilities for two drums. The dose-minimizing arrangement for the higher specific activity drum to be placed on top is given for the coloured region. The colour corresponds to the level of resulting dose rate benefit when using the high dose rate drum 3 (red is higher benefit).

This rather simple example shows that for a true dose rate minimization, all radiological properties must be taken into account; no univariate rule suffices. For more stacking levels, more nuclides and most importantly more positions the identification of the dose minimizing arrangement can be tedious. Here, we demonstrate a strategy to potentially drastically minimize the local dose rates in a low and medium activity waste (MAW / LAW) storage facility with approx. 1500 waste packages and over 2000 positions; this reduction is achieved by maximizing shielding effects by all packages.

The MAW/LAW storage facility of the JEN GmbH

Storage facility

The drums are stored in 65 chambers, each hosted by one of 10 so called cells; a cell contains up to 38 chambers. The chambers in total differ in geometry, especially in height and thickness of the covering shielding slabs. Depending on the chamber’s height, drums can be stacked in 1, 2 or 3 layers. 

Waste in drums

The largest part of the waste packages are drums (there also exist a few samples, which shall all but be ignored). The drums contain flammable and non-flammable waste, waste with volatile components, solid and liquid waste.

The drums are fully radiologically characterised, with dose rate measurements at the surface and in 1 m distance. In addition, nuclide specific activities and masses of fissile nuclides exist. The quality of the radiological characterization varies, with newer waste being more accurately and fully characterized. Old waste (40 years) may display data deficiencies in that only a limited number of nuclides are evaluated or that the waste package mass is not recorded.

Regulatory constraints

As for the regulatory environment, there exist a large number of constraints, limiting the activity and masses of individual nuclides and groups of nuclides, depending on the waste type. The constraints are valid for individual cells, chambers and the entire facility. In total, there are 111 individual constraints that must be respected.

Validation of the optimizer

Validation of exhaustion of activities and masses

Before any optimization can be performed, it is essential to verify that the optimizer assesses the current arrangement of drums in the storage facility (which shall hereafter be referred to as the “reference arrangement”) in the same way the JEN-internal storage facility management application does. To this end, the same data set was fed to both the optimizer and this management application and the results (exhaustion of activities and masses of nuclide groups with respect to the constraints) were compared. The comparison yielded excellent agreement.

We therefore conclude that the constraints are properly implemented in the optimizer and that the physical and radiological properties are read correctly.

Validation of the dose rate calculation

The stacked-layer approximation

In analogy to the previous section, a minimization of dose rate can only take place if the optimizer’s dose rate module, which calculates the dose rate above every chamber for a given drum arrangement, is able to reproduce the dose rate of the reference arrangement. Due to the prohibitively high local dose rate above some chambers, the local dose rate was measured at specified locations directly above 4 chambers, at locations P1 to P4.

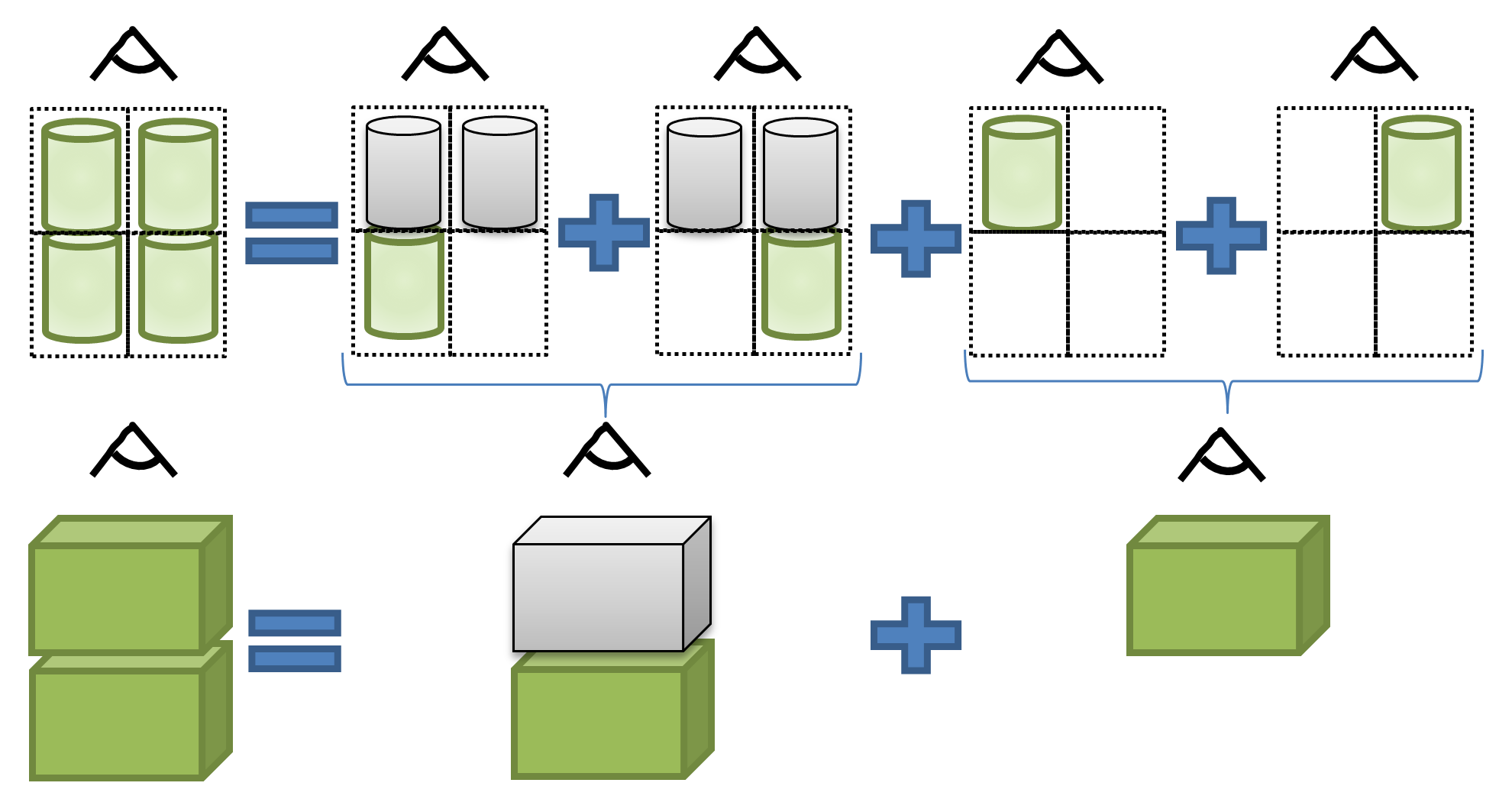
In principle, the calculation of the dose rate for a given drum arrangement using a point-kernel integration, e.g., MicroShield® [2], necessitates the modelling of every single drum as an emitter, and using all other drums between the emitting drum and the computation point as shields, see Figure 2, above. For every new arrangement of the drums, a dose rate calculation requires n new individual calculations, with n being the number of drums. Matters are further complicated when in addition having to determine all shielding drums between the emitting drum and the calculation point.

To simplify modelling, the drums’ properties in any one layer are aggregated to effective values: Here, the gamma-emitting activities and masses are combined to yield effective densities (mass in the layer divided by the layer volume) and activities (sum of nuclide specific activity per layer), see Figure 2, below. The number of calculations required decreases to the number of layers considered.

Figure 1: Simple arrangement possibilities for two drums. The dose-minimizing arrangement for the higher specific activity drum to be placed on top is given for the coloured region. The colour corresponds to the level of resulting dose rate benefit when using the high dose rate drum 3 (red is higher benefit).

Validation of the stacked-layer approximation

The stacked-layer approximation was validated by four dose rate measurements at locations P1 through P4 above the concrete shielding slabs (cf. Figure 3). The pictures above the plot show pictures of the measurement points P1 and P2. The calculations themselves are performed with MicroShield®, the agreement to the calculation is favourable for P4 and P3 with the stacked-layer approximation, faithfully reproducing the measured dose rates. For P2, the dose rate is overestimated by about a factor 3 to 4. We tentatively attribute this to data quality. A more detailed investigation showed that drums of that chamber are mostly very old (~40 y) and poorly characterized (not shown). For the same reason the agreement of measured and calculated values of P1 is very poor; the calculation underestimates the measurement by an order of magnitude.

We therefore conclude that the stacked-layer approximation provides a reasonable estimation for the measured dose rates, but that the quality of agreement is commensurate with the underlying quality of data.

Figure 3: Validation of the stacked layer approximation

To be useful in the optimizer, the estimation of the dose rate from a given chamber must take place as fast as possible, at least at a rate of several thousands of calculations per second on off-the-shelf computers. To accelerate calculation times therefore, the stacked-layer model was parametrized to a linear expression, taking only µs to calculate. To this end, for every chamber and layer, dose rate conversion factors were pre-calculated for two key nuclides, Co-60 and Cs-137. Some accuracy is sacrificed for the benefit of speed, since the generated linear expression serves only as an approximation to the point-kernel integration by MicroShield®.

Validation of the parametrized stacked layer approximation

A comparison between the stacked layer approximation and the parametrized stacked layer approximation is shown in Figure 4. The data underlying this comparison was snapshot at a later point in time than that of Figure 3. Here, results of the stacked layer approximation as calculated with MicroShield® are shown as the bars without fill, the filled bars are the corresponding parametrized calculations. In general the correlation is good, especially taking into account the large dynamic range of the results. The parametrization tends to underestimate the dose rate; at most it disagrees by about 50 % with respect to the corresponding MicroShield® calculation (P3).

In conclusion, the agreement of the parametrized stacked-layer approximation is reasonable. Hence, it was used in the dose rate module of the optimizer.

Minimization of dose rates with the optimizer

The optimizer was configured to rearrange drums of the chambers corresponding to P1 to P4, while respecting the regulatory constraints for these chambers. Additional constraints were set up to prevent ‘floating’ drums, i.e. drums positioned in the middle or top layer without corresponding drums in the lower layer(s). The minimization variable is set to be the sum of all four dose rates.

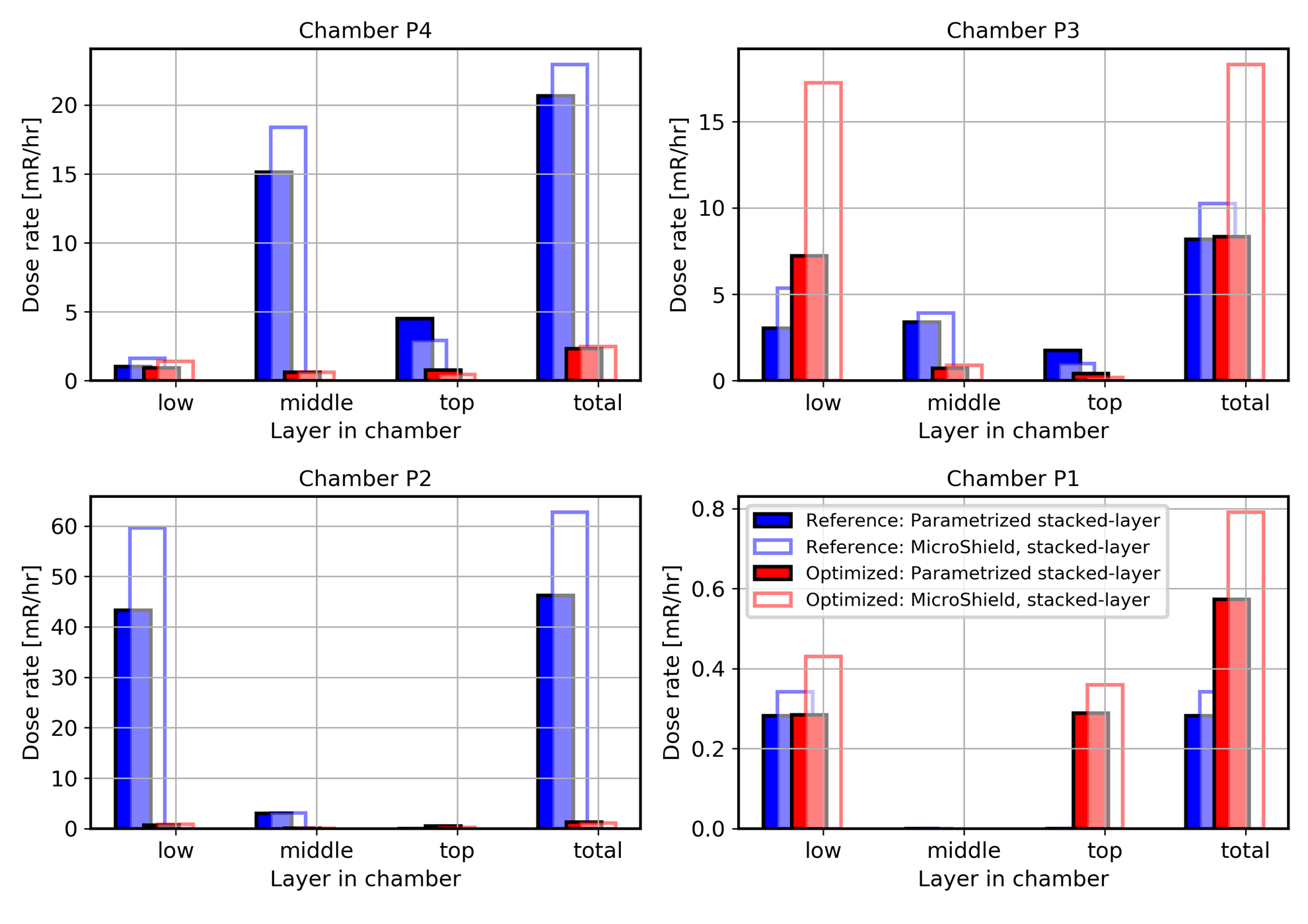
Figure 4: Dose rates of 4 chambers P1 through P4 before (blue) and after (red) the optimization run, calculated both with a point-kernel integration (MicroShield) of the stacked-layer approximation (no fill) and with our parametrized stacked-layer approximation (solid fill)

Figure 4 shows the results of the dose rates, both before and after the optimization run. In P1, no reduction is achieved, on the contrary: the dose rate approximately doubles, from 0.3 mR/hr to about 0.6 mR/hr[1]. Similarly, the dose rate of P3 remains essentially constant at 8 mR/hr (parametrized stacked-layer approximation) or even increases, from about 10 mR/hr to nearly 20 mR/hr (MicroShield® – calculation). In the two chambers with an initially higher dose rate, P4 (approx. 20 mR/hr) and P2 (between 45 and 60 mR/hr), the dose rate decreases by one or even two orders of magnitude, respectively. Since these two chambers contribute the lion’s share to the initial dose rate, the marked decrease also has the most profound effect on the sum of all dose rates: The sum of dose rates over all chambers decreases to between 16 % (parametrized stacked-layer approximation) and 24 % (MicroShield®) of its initial value (Figure 5). We note that all regulatory constraints are respected for the optimized arrangement.

Figure 5: Cumulative dose rate reduction over 4 chambers between reference and optimized state

A closer inspection reveals that there is a net flow of mass and activity to chamber P3 (not shown); all other chambers experience a drain. This is not surprising, since chamber P3 has the lowest dose rate conversion factors owing to the thickest shielding slabs of all 4 chambers.

The mass is concentrated in the upper layers, while the activity is distributed primarily in lower layers. Co-60 with the higher dose rate conversion factor, is distributed nearly exclusively in the lowest layer.

Pareto Scoring: Simultaneous minimization of dose rates and working time required for drum rearrangement

Relocation time effort

Unfortunately, the repositioning of drums to the fully optimized state is infeasible, since a large number of drums would have to be manipulated, which will cause unjustifiably high doses to the personnel that will have to handle the concrete slabs shielding the storage cells and the waste packages with remote-controlled lifting equipment. We therefore seek to limit the time spent relocating the drums at the same time as minimizing the dose rates.

A matrix of time costs was compiled, detailing the times required to emplace or to remove a drum from a certain position. Furthermore, times were associated with the first of such a manipulation; these times are only counted once. All available drum positions in the entire storage facility were accounted for in this way.

Since no weighting variable could be identified which linked the dose rate sum and the working time, the optimizer was provided with two separate optimization variables: the sum of all dose rates, and the total working time. The optimizer searches for minima of the working time for a given dose rate sum, and for a minimum of the dose rate sum for a given working time.

Optimization

Figure 6 shows the result of such a Pareto optimization. For low permitted relocation times, the achievable dose rate reduction (dashed line) is limited. For higher permitted times, the possible dose rate reduction increases. For the highest time, the dose rate reduction can approximate two orders of magnitude.

When offering the optimizer the current drum arrangement as a starting value (blue diamonds), the optimizer converges on a much lower value compared to optimizing from an uninitialized state (red squares). The reason for this is that the optimizer must spend time excluding forbidden constraints when starting from an uninitialized state, time that is lost for performing dose rate optimizations.

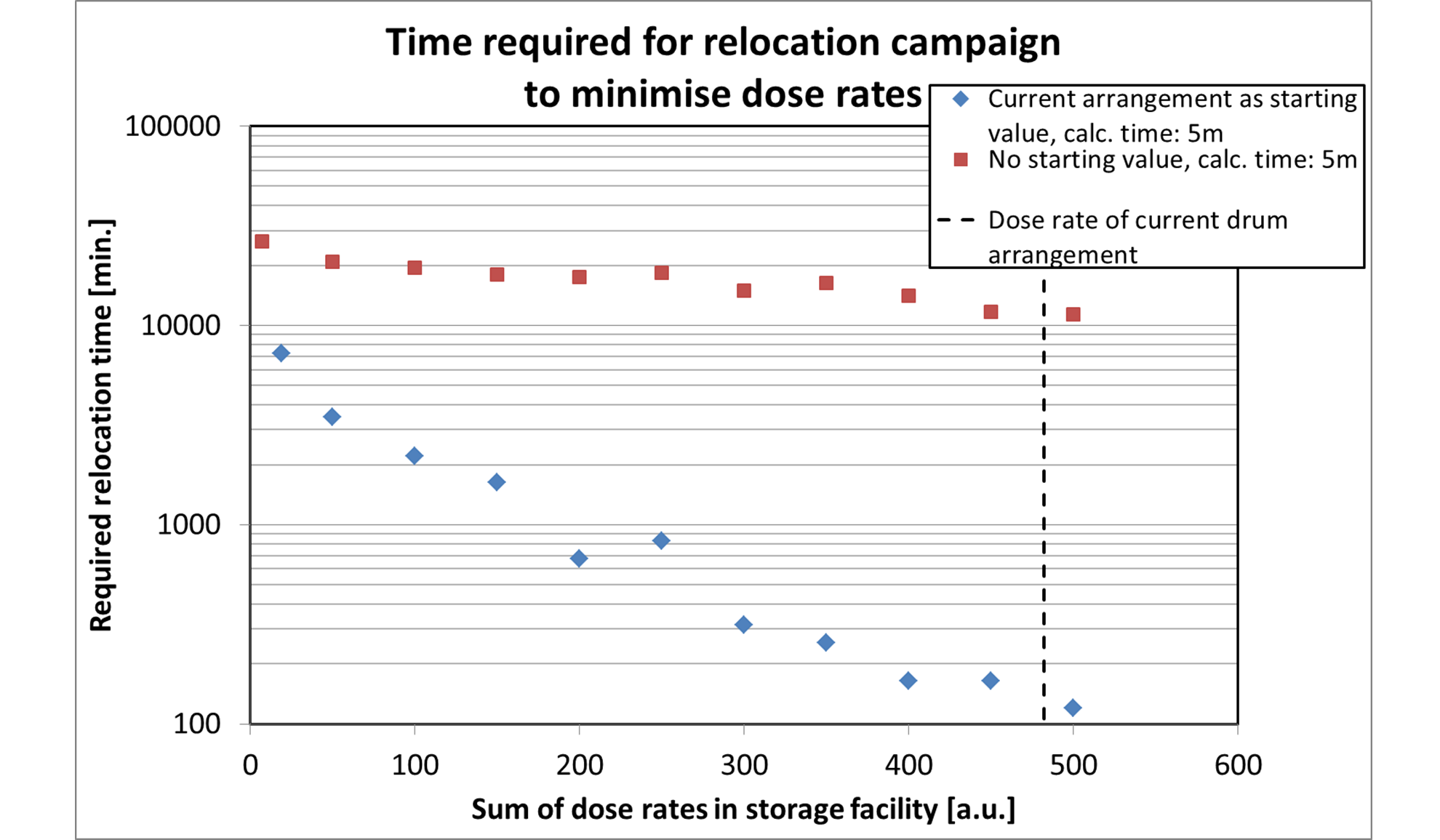
Figure 6: Pareto plot of the two minimization variables sum of dose rates and relocation time

Conclusion and Outlook

We demonstrated that close to an order-of-magnitude reduction in local dose rates is possible in four reference chambers, by simply rearranging drums to exploit (self-)attenuation to the largest extent in a given calculation time, while respecting a large number of complex constraints given by the regulatory environment. The optimization itself was performed by a constraint satisfaction solver, with the sum of the local dose rates as minimization variable. The solutions were identified in a matter of minutes.

When performing the optimization for drums from all 65 chambers in the JEN MAW / LAW facility, a reduction by up to 2 orders of magnitude can be achieved at the cost of a relocation time of several hundred hours, a forbiddingly high effort. For lower relocation times, the dose rate reduction can still be substantial.

In the context of this facility, results of this optimization may carefully be applied during the maintenance of the cells, when the manipulation of the drums becomes necessary anyway. Here, for a limited number of drums, an optimization can at least reduce dose rates of single chambers. Prior to any optimization calculation, the validity and consistency of the underlying data will have to be reviewed.

We foresee widespread potential for the optimization techniques demonstrated here in radwaste inventory bookkeeping tools and in the identification of dose-minimizing storage facility decommissioning strategies. Note that due to decay, the dose-minimal arrangement is likely to change over time; the solver then facilitates identification of minimal dose rate configurations even below the rate governed by decay.

The solver that is used for performing the optimisation is implemented on top of an open-source optimizer, to which site-specific constraints and optimization goals have to be fitted. Once prepared, optimization runs are a matter of a few minutes up to a few hours (depending on the complexity of the constraints and optimization goals) and thus allow analysis of multiple configurations in a reasonable period.

Acknowledgements

The authors would like to thank Gert Hoppe, Dr. Yevgeniy Shapiro and Dr. Ralf Kunz (Brenk Systemplanung) for help with preparing the data and for interesting discussions. The author also thanks Rebekka Gehr (Brenk Systemplanung) for carefully proofreading the manuscript.

The author likes to thank the Federal Ministry of Education and Research for the support of this research project under the support code 15 S 9400. Responsible for the content of this presentation is the author.

References

[1]          V. G. Rudychev, N. A. Azarenkov, I. A. Girka, and E. V. Rudychev, Irradiation dose minimization by optimizing the arrangement of radiation sources of different intensity, Atomic Energy Vol 119 No. 4, DOI 10.1007/s10512-016-0061-7

[2]          Grove Software, Microshield Version 8.03, Copyright 1995 – 2009

[1] The units “mR/hr” (milli Röntgen per hour) is a legacy unit for radiation exposure still in use by MicroShield®; the units used are completely irrelevant to the discussion.